How To Find The Area Of A Parallelogram Using Diagonals

What is a Parallelogram?

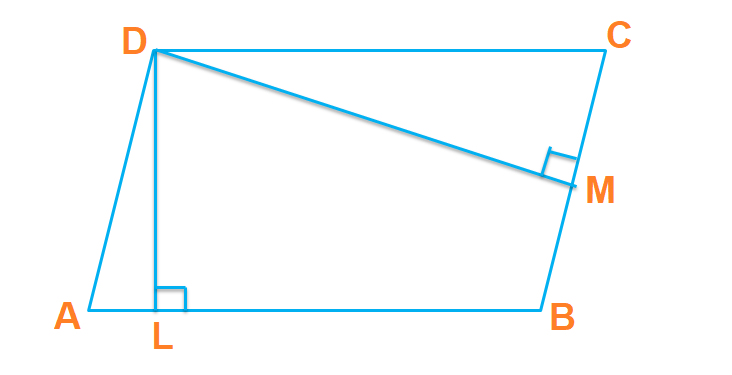
A parallelogram is a quadrilateral, whose each pair of opposite sides is parallel. Suppose we accept a parallelogram ABCD such that AB and DC are a pair of its reverse sides and so that AB ‖ BC. Similarly, BC and AD are a pair of opposite sides such that BC ‖ AD.

Properties of a Parallelogram

We now know that a parallelogram is a quadrilateral, whose each pair of opposite sides is parallel too equally equal. Below are some properties of a parallelogram that assist united states in dissimilar calculations including finding its area under unlike conditions:

The opposite sides of a parallelogram are parallel and equal to each other.
Since the parallelogram is a quadrilateral, the sum of all its angles is 360^o
The reverse angles of a parallelogram are equal. This means that for a parallelogram ABCD, the angle formed at vertex B would be equal to the angle formed at vertex D. Similarly, the angle formed at vertex A would be equal to the angle formed at vertex C.
The adjacent angles of a parallelogram are supplementary, i.e. the sum of the adjacent angles of a parallelogram equals 180^o. This means that for a parallelogram ABCD, the bending formed at vertex B + angle formed at vertex C = 180^o. Similarly, the angle formed at vertex A + angle formed at vertex B = 180^o.
Diagonal of a parallelogram bisect each other.
Rectangle, square and rhombus are special types of parallelograms.

Finding Area of a Parallelogram

Permit usa consider the in a higher place parallelogram, ABCD. If DL ⟂AB, then any line, so nosotros find whatsoever line segment with its cease-points on the two sides AB and DC perpendicular to them has the length DL. Then, we call AB equally the base and DL the corresponding altitude.

Similarly, if DM ⟂BC, then whatever line segment with its cease-points on the ii sides AB and DC perpendicular to them has the length DM. so we can telephone call BC every bit the base of operations and DM every bit the respective distance.

We take,

Area of a parallelogram = Base x Altitude

Distance is also known equally height. So, we can say that,

Area of a parallelogram = Base of operations x Height

For example, let us find the area of a parallelogram having the base of operations = 5 cm and altitude = 4.2 cm.

We know that

Area of a parallelogram = Base 10 Distance

Here, base = 5 cm and altitude = 4.2 cm

Therefore,

Area = (5 10 4.2) cm^{2 =}21 cm²

Solved Examples

Case 1

A mirror is made of two congruent parallelograms as shown in the diagram. The parallelograms have a combined expanse of 9 1/3 square metres. The height of each parallelogram is ane 1/3 metres. What is the length of the base of each parallelogram?

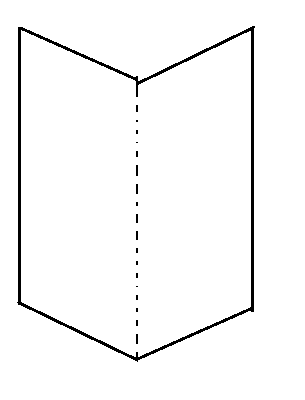
Solution: We have been given that the mirror is made of two congruent parallelograms. Since the given parallelograms are congruent, therefore, the expanse of ii parallelograms will exist equal.

Hence, nosotros can say that,

The total area of the two parallelograms = $ix\frac{1}{iii}$ thousand²

The total expanse of the 2 parallelograms = $\frac{28}{three}$ m²

Therefore,

Area of one parallelogram = $\frac{28}{three}$ thou² ÷ two

Expanse of one parallelogram = $\frac{14}{3}$ 1000^two

Now, nosotros know that,

Area of a parallelogram = Base x Height

Also, nosotros have been given that the elevation of each parallelogram is $1\frac{1}{iii}$ k

Superlative = $1\frac{1}{3}$ m = $\frac{four}{3}$ chiliad

Hence, past putting the values of the area of one parallelogram and pinnacle in the to a higher place formula, we get,

$\frac{14}{3}$ = Base x $\frac{iv}{three}$

⇒ Base of operations = $\frac{xiv}{three}\times \frac{3}{four}$ thou

⇒ Base = $\frac{7}{two}$ m = $3\frac{one}{ii}$ m

Hence, base of operations of the each parallelogram = $3\frac{1}{2}$ k

Example 2

The base of operations of a parallelogram is thrice its superlative. If the surface area of the parallelogram is 867 m², find the base of operations and the height of the parallelogram.

Solution: We take been given that the area of the parallelogram is 867 1000².

Also,

The base of a parallelogram is thrice its superlative. Permit the summit of the parallelogram be h cm. And then,

The base of the parallelogram will exist 3h

At present, nosotros know that

Area of a parallelogram = Base x Superlative

Putting the given values in the above formula we become,

867 = 3h ten h

⇒ 3h2 = 867

⇒ h2 = 289

⇒ h = $\sqrt{289}$

⇒ h = 17 cm

Now, that we know the elevation of the parallelogram, nosotros tin find the base as well

Base of the parallelogram = 3h = iii 10 17 = 51 cm.

Hence, base of the parallelogram = 51 cm, height of the parallelogram = 17 cm.

Case 3

A field in the form of a parallelogram has a base 15 dam and altitude eight dam. Observe the toll of watering the field at the charge per unit of 50p per square metre.

Solution: Nosotros accept been given that,

The base of operations of the field = 15 dam

The distance of the field = eight dam

We need to find the cost of watering the field at the rate of 50p per square metre. Note: the above units are in dam, while we need to calculate the cost of watering the field in mⁱⁱ. Therefore, we must first convert these units to metres.

Nosotros know that

1 dam = 10m

Therefore,

Base of the field = xv dam = 150 thousand

Distance of the field = 8 dam = 80 m

Now, to find the cost of watering the field at the rate of 50p per square metre, we need to observe the area of the parallelogram.

We know that

Surface area of a parallelogram = Base x Height

Putting the given values in the above formula we become,

Area of the field = (150 x lxxx) m² = 12000 1000²

Rate of watering the field = 50p per square metre = £0.5 per square metre

Therefore,

Price of watering the field at the charge per unit of 50p per square metre = £(12000 10 0.5)

=£6000

Hence, the toll of watering the field at the rate of 50p per one thousand² = £6000

Case 4

In a parallelogram, ABCD, CM ⟂ AB and BL ⟂ AD

a) If AB = 16 cm, Advertising = 12 cm and CM = 10 cm, notice BL

b) If Advertising = 10 cm, CM = eight cm and BL = 12 cm, discover AB

Solution:

a) Showtime, nosotros should describe the given parallelogram and understand what is given to us.

Therefore, we take the following parallelogram

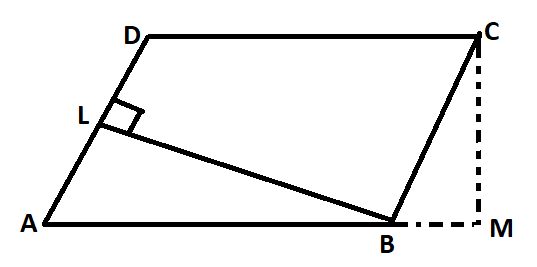
At present, we have been given that AB = 16 cm, Advert = 12 cm and CM = 10 cm. Nosotros demand to find BL.

In the given parallelogram, we can conspicuously see that AB is one of the bases and CM is the respective altitude.

We know that

Area of a parallelogram = Base x Height

Putting the given values in the above formula we go,

Area of the parallelogram ABCD = (sixteen ten 10) cm^two = 160 cm²

Since we have BL as the altitude to the side AD, therefore, AD tin can also be used as a base of the parallelogram. This means that some other fashion to computing the expanse of this parallelogram is to use Advertizement every bit the base of operations and BL as the corresponding meridian.

Thus,

Area of the parallelogram ABCD = Advert ten BL

⇒ Area of the parallelogram ABCD = 12 10 BL

Now, the two areas thus obtained are of the same parallelogram and therefore should be equal. We now have,

12 10 BL = 160

⇒ BL = 160/12 = xiii.33 cm

Hence BL = 13.33 cm

b) Nosotros have been given that Advertising = x cm, CM = 8 cm and BL = 12 cm. Nosotros need to find AB.

Once more, the diagrammatic representation of this parallelogram shall exist the same equally in the in a higher place part.

Therefore, in the given parallelogram, we can clearly meet that Advertising is one of the bases and BL is the corresponding altitude.

Nosotros know that

Area of a parallelogram = Base ten Peak

Putting the given values in the above formula we get,

Surface area of the parallelogram ABCD = (10 x 12) cm² = 120 cm²

Since we accept CM equally the altitude to the side AB, therefore, AB tin likewise be used as a base of the parallelogram. This means that another mode to calculating the surface area of this parallelogram is to use AB as the base of operations and CM as the corresponding height.

Thus,

Area of the parallelogram ABCD = AB x CM

⇒ Area of the parallelogram ABCD = AB x 8

Now, the two areas thus obtained are of the aforementioned parallelogram and therefore should be equal. We at present have,

AB x 8 = 120

⇒ AB = 120/viii = 15 cm

Hence AB = 15 cm

Example 5

The longer side of a parallelogram is 54 cm and the corresponding altitude is 16 cm. If the altitude corresponding to the shorter side is 24 cm, detect the length of the shorter side.

Solution: Let ABCD be a parallelogram with the longer side AB = 54 cm and corresponding altitude AE = 16 cm.

Diagrammatically, the given parallelogram can be represented as:

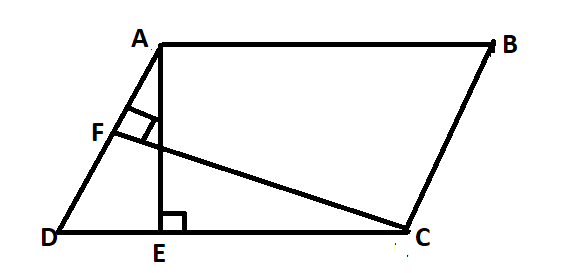
The higher up diagram shows that the shorter side is BC and the corresponding distance is CF. At present we are given that the distance corresponding to the shorter side is 24 cm. therefore,

CF = 24 cm

Also, we are given the longer side of a parallelogram. Therefore,

AB = CD = 54 cm

Also, and the corresponding altitude to the longer side is 16 cm. therefore,

AE = 16 cm

We know that

Area of a parallelogram = Base ten Height

We have two sets of bases and the respective altitudes. Therefore, we can say that –

Expanse of a parallelogram = BC x CF……………………….. (one)

and

Area of a parallelogram = AB x AE………………………………(ii)

Since both (1) and (2) represent the area of the same parallelogram they should be equal. Hence, equating the equations (1) and (2), we have

BC x CF = AB x AE

At present, nosotros already have, AB = 54 cm, CF = 24 cm and AE = 16 cm. putting these values in the above equation, we have

BC x 24 = 54 x 16

⇒ BC = $\frac{54\times16}{24}$ = 36 cm

Hence, the shorter side of the parallelogram, i.e. BC = 36 cm

Example 6

A floral blueprint on the floor of a building consists of 280 tiles. Each tile is in the shape of a parallelogram of distance 3 cm and base of operations v cm. Find the cost of polishing the pattern at the rate of 50 p per cmⁱⁱ.

Solution : Nosotros have been given that the floral design on the floor of a edifice consists of 280 tiles. Besides, each tile is in the shape of a parallelogram of altitude three cm and base v cm.

Nosotros need to find the toll of polishing the design at the rate of 50 p per cmⁱⁱ.

In order to do so, we must first calculate the area covered by the tiles.

Therefore, first, nosotros must calculate the area covered by i tile.

Since, the tile is in the shape of a parallelogram,

Area of 1 tile = Base x Top

Base of operations of the tile = 5 cm

Elevation of the tile = 3 cm

Hence, Area of one tile = (5 ten 3) cm² = 15 cmⁱⁱ

At present. Total number of tiles = 280

Area covered past 280 tiles = (280 x xv) cm² = 4200 cm^two

Price of polishing the design = 50 p per cm² = £0.v per cm²

Cost of polishing 4200 cm² = £ (0.five ten 4200) = £2100

Hence price of polishing the design at the charge per unit of 50 p per cm² = £2100

Case 7

Observe the altitude of a parallelogram in metres whose surface area = 2.25 m^two and base is 25 dm.

Solution: We have been given that the area of the parallelogram= 2.25 m²

Also, base of the parallelogram = 25dm

Note the change in dimensions. Before proceeding farther, we must kickoff ensure that all the given values are in the same dimensions.

We know that 1 m = 10 dm

Therefore

1 dm = 1/10 m

25 dm = 25/10 thousand = 2.5 m

Now, we know that

Expanse of a parallelogram = Base x Superlative

Putting the given values in the above formula we become,

2.25 = two.v x Meridian

Meridian = two.25/two.5 m = 0.9 m

Hence, the peak of the parallelogram = 0.ix m

Example 8

The adjacent sides of a parallelogram are ten thou and 8 chiliad. If the distance between the longer sides is 4 m, find the altitude betwixt the shorter sides.

Solution: Let ABCD be a parallelogram with the longer side AB and shorter side BC.

Diagrammatically, the given parallelogram tin be represented every bit:

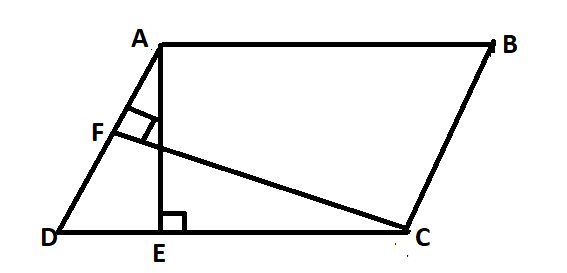
The to a higher place diagram shows that the distance between the longer sides, AB and DC is AE which is given to as four m. Now we are given that the altitude corresponding to the longer side is 4 cm. therefore,

AE = 4 cm

Besides, we are given the longer side of a parallelogram. Therefore,

AB = CD = x cm

Also, and the shorter side of the parallelogram BC is also given to the states. Therefore,

BC = 8 cm

We know that

Area of a parallelogram = Base x Top

Nosotros have two sets of bases and the corresponding altitudes. Therefore, we tin say that –

Surface area of a parallelogram = BC x CF……………………….. (1)

and

Area of a parallelogram = AB ten AE………………………………(2)

Since both (one) and (2) represent the area of the same parallelogram they should exist equal. Hence, equating the equations (one) and (ii), we accept

BC ten CF = AB x AE

At present, we already accept, AB = 10 cm, BC = eight cm and AE = 4 cm. putting these values in the above equation, we have

eight x CF = 10 x 4

⇒ CF = $\frac{x\times4}{8}$ = 5 cm

Hence, the distance between the shorter sides of the parallelogram, i.e. CF = v cm

Example 9

The surface area of a parallelogram is 338 m². If its altitude is twice the corresponding base, make up one's mind the base and the distance.

Solution: We have been given that the area of the parallelogram is 338 m^two.

Also, the altitude is twice the corresponding base.

Let the base of the parallelogram exist b cm. Then co-ordinate to the condition given in the question,

The altitude of the parallelogram = 2b

We know that

Area of a parallelogram = Base x Height

Putting the given values in the above formula nosotros get,

338 = b x 2b

2b² = 338

b² = 338/two = 169

b = $\sqrt{169}$ = 13 cm

Hence, base of the parallelogram = 13 cm.

Now, that we know the base of the parallelogram, we can discover the height as well

Height of the parallelogram = 2b = 2 ten 13 = 26 cm

Hence, base of the parallelogram = 13 cm, summit of the parallelogram = 26 cm.

Recommended Worksheets

Area of Other Quadrilaterals (Province Themed) Math Worksheets
Quadrilaterals (Real Estate Themed) Math Worksheets
Word Bug Involving Perimeter and Area of Polygons (Carpentry Themed) Worksheets

We spend a lot of fourth dimension researching and compiling the information on this site. If y'all find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!