How To Find Test Statistic For Hypothesis Test

In our example concerning the mean grade point boilerplate, suppose we take a random sample of northward = fifteen students majoring in mathematics. Since due north = fifteen, our test statistic t* has n - one = xiv degrees of liberty. Also, suppose we set our significance level α at 0.05, so that we have only a 5% hazard of making a Blazon I fault.

Correct-Tailed

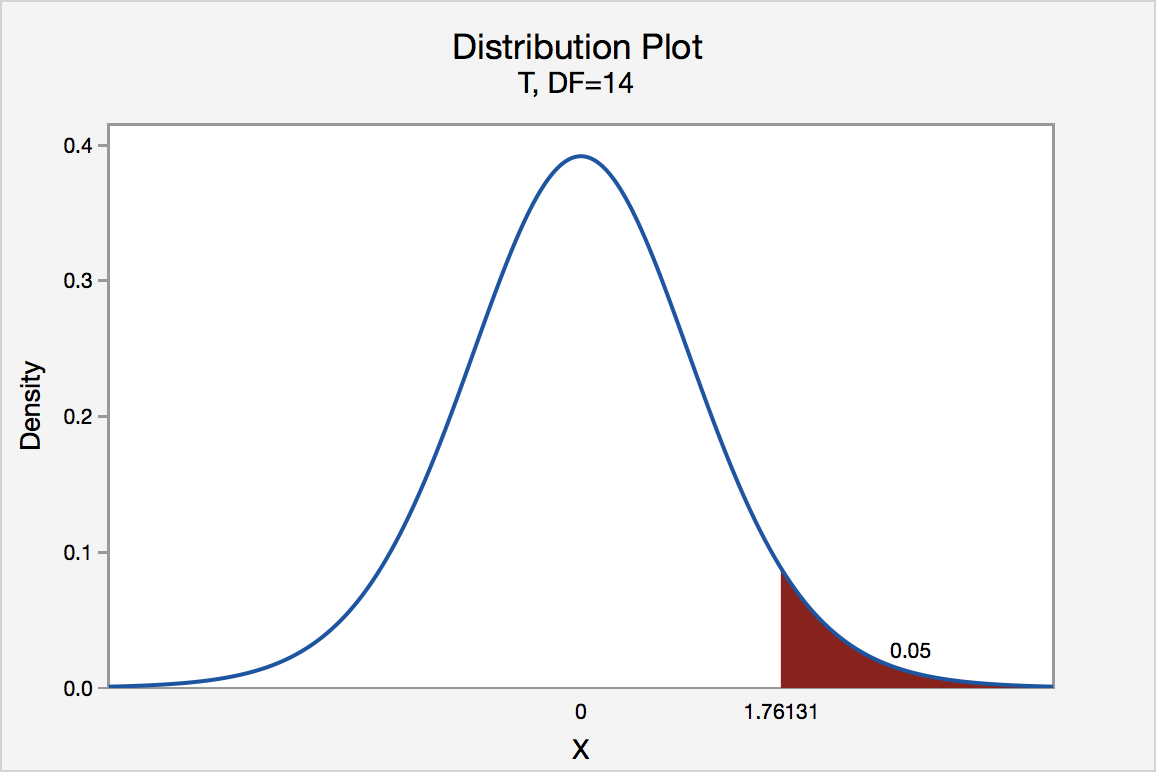
The critical value for conducting the correct-tailed test H ₀ : μ = 3 versus H _A : μ > 3 is the t-value, denoted t _\(\alpha\) , n - 1, such that the probability to the right of it is \(\alpha\). It can be shown using either statistical software or a t-table that the critical value t _{0.05,fourteen} is 1.7613. That is, we would reject the null hypothesis H ₀ : μ = 3 in favor of the culling hypothesis H _A : μ > 3 if the test statistic t* is greater than ane.7613. Visually, the rejection region is shaded red in the graph.

t distribution graph for a t value of 1.76131

Left-Tailed

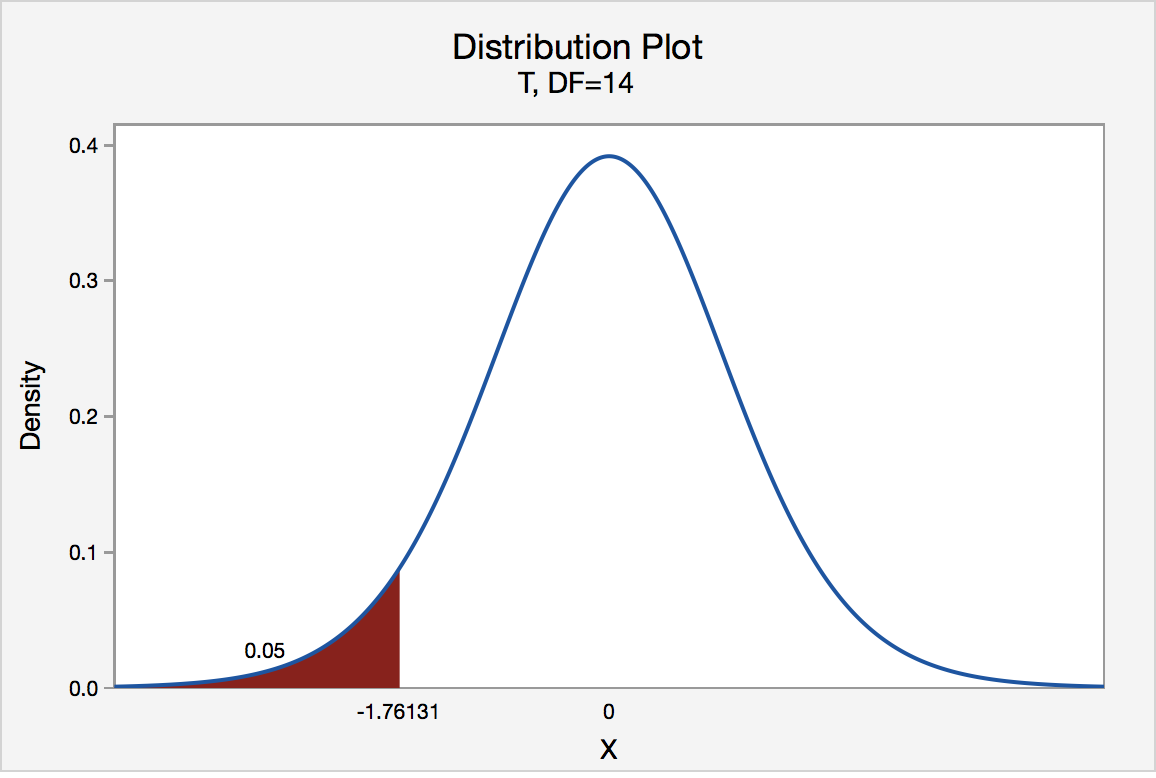
The critical value for conducting the left-tailed test H ₀ : μ = three versus H _A : μ < 3 is the t-value, denoted -t _{(\(\alpha\), northward - 1)} , such that the probability to the left of information technology is \(\alpha\). It can be shown using either statistical software or a t-table that the critical value -t _0.05,xiv is -1.7613. That is, we would decline the null hypothesis H ₀ : μ = 3 in favor of the alternative hypothesis H _A : μ < 3 if the test statistic t* is less than -1.7613. Visually, the rejection region is shaded scarlet in the graph.

t-distribution graph for a t value of -1.76131

Ii-Tailed

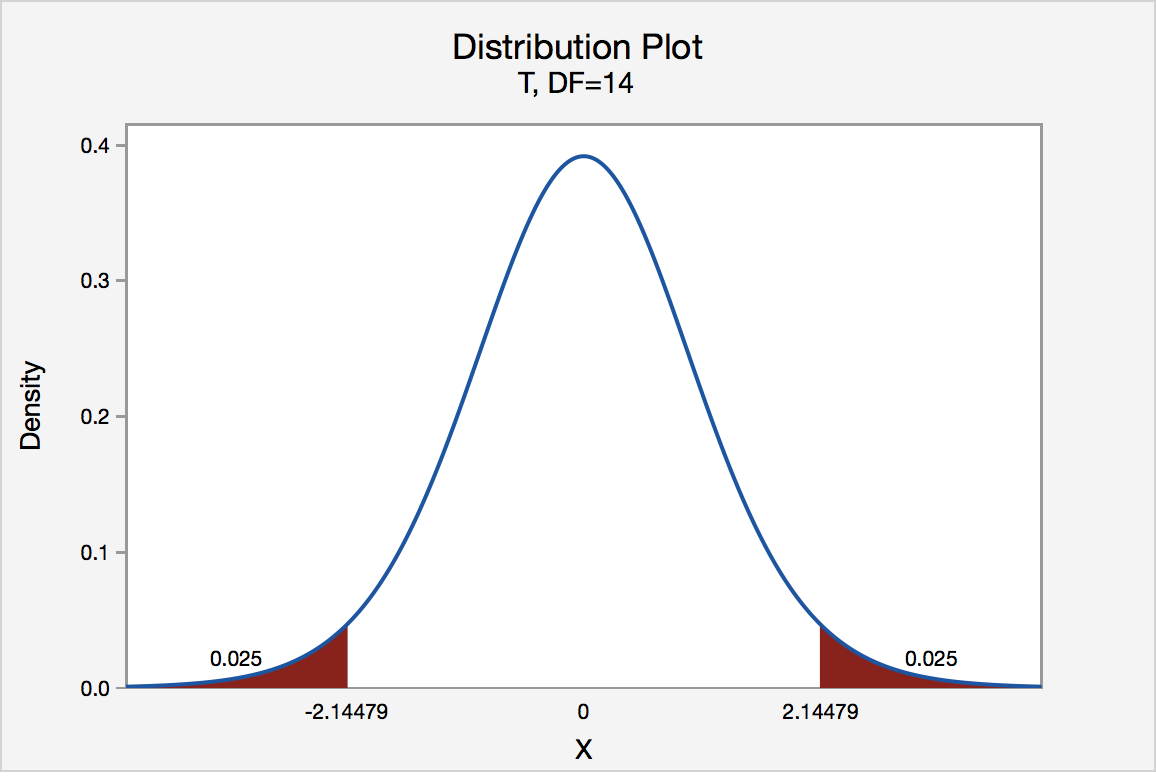
There are ii disquisitional values for the 2-tailed test H ₀ : μ = three versus H _A : μ ≠ 3 — 1 for the left-tail denoted -t _{(\(\alpha\) _/2, n - 1)}and one for the right-tail denoted t _{(\(\alpha\) _/2, n - i)}. The value - t _{(\(\alpha\)/2, due north - i)} is the t-value such that the probability to the left of it is \(\blastoff\)/2, and the value t _{(\(\alpha\)/2, n - 1)} is the t-value such that the probability to the right of information technology is \(\blastoff\)/2. Information technology can be shown using either statistical software or a t-table that the disquisitional value -t _0.025,14 is -2.1448 and the critical value t _0.025,14 is ii.1448. That is, nosotros would reject the nix hypothesis H ₀ : μ = 3 in favor of the alternative hypothesis H _A : μ ≠ 3 if the exam statistic t* is less than -2.1448 or greater than two.1448. Visually, the rejection region is shaded red in the graph.